와! 몇개월만의 부활! 허리가 이젠 좀 괜찮아져서.. 흑흑
책상에 앉아 봅니다.
앉은김에 가볍게 뭣 좀 해보죠.
오늘 볼 것은 바로 빌보드 (Billboard) 인데요,
이걸 설명하기 전에 알아야 할 지식이 좀 있습니다.
버텍스 셰이더의 MVP 변환에 대해 아셔야 해요. 다른 말로 하면 렌더링 파이프라인.
렌더링 파이프라인 : 버텍스 변환
나중에 다시 설명할 날이 있을지도 모르겠지만 지금 필요하니까 간단히 설명을 하자면 이 변환은
로컬 좌표계 -> 월드 좌표계 -> 카메라 좌표계 -> 프로젝션 좌표계로 변환하는 것을 의미하는데요
로컬 좌표계
물체가 가지고 있는 고유의 좌표계를 의미합니다. 이 상황에서 물체는 자기 피봇점이 0,0,0 포인트이며, 자기 자신이 즉 좌표계입니다.

월드 좌표계
물체는 더이상 자기가 중심이 아니며, 월드의 어느 한 점이 중심이 됩니다.
즉 로컬 좌표계에서 월드 좌표계를 곱해주면, 각 버텍스들은 회전과 이동을 해서 월드에 배열되게 됩니다.

카메라 (뷰) 좌표계
여기서는 카메라가 중심입니다. 월드 좌표계에 있던 버텍스들은 회전하고 이동하여 카메라에서 바라보는 방향으로 재 배열됩니다


프로젝션 좌표계
거리가 멀면 작아져야겠죠? 거리에 따라 작아지는 연산이 들어가 있습니다.


좋아요 너무 허접하게 좌표계 설명을 했네요.
좌표 변환 (공간 변환) 에서는 각 기준점에 맞춰 버텍스가 이동이나 회전을 한다는게 핵심입니다. 뭐.. 행렬 연산이라는게 원래 그러라고 만들어 놓은거니까요
뻔히 아는건데 왜 설명을 하냐? 여기에서 빌보드 기술의 핵심이 생기기 때문입니다.
뷰 공간의 입장을 일단 들어봅시다
일단 월드에서 뷰 변환할때 일어나는 일을 생각해 봅시다. 우리가 아는 월드 뷰의 모습은 이렇지요

아 .. 그런데, 이게 지금 사실은 월드 뷰의 모습이 아닙니다. 카메라에 프로젝션까지 변환이 끝난 뷰라서 우리가 카메라로 보고 있는 거죠. 즉 프로젝션 뷰의 상태의 최종 모습니다. 저 기즈모만 없다고 다시 생각해 보세요.

이게 월드뷰입니까? 아니죠. 지금 보이는 화면은 아무리 봐도 프로젝션 뷰입니다 .
프로젝트션 뷰에서 카메라 뷰로 바꿔볼까요
그럼 이렇게 보입니다. 원근감은 없고, 박스는 '회전' 해서 한 45도로 있지요? 이게 카메라 좌표계(공간) 상태입니다!

굳이 기즈모를 보셔야 마음이 편하시겠다고 생각하신다면 이거죠 . 좋아요. 이게 카메라 공간입니다.
카메라 공간 기준에서는 ... 저 박스들은 '기울어' 져 있는겁니다. 맞죠?

이번에는 월드 공간 입장에서 봅시다.
월드 공간은 사실 볼 수가 없어요. 왜냐? 카메라가 없으니까!!!

그런데 만약 본다고 쳐 봅시다. 억지로.
월드 공간이 카메라라고 생각해 보는거죠.
그럼 이런 모습이 됩니다. 프론트 뷰랑 같은 모양이 되는거죠.
어라? 월드 공간을 억지로라도 카메라로 보면 프론트 뷰가 된다? 여기서 빌보드의 힌트가 시작됩니다.

월드 공간에서 뷰 공간으로 변화할때 그럼 무슨 일이 일어나냐?
자 월드 공간에 잘 지내던 녀석이 카메라 공간으로 변환되면 무슨 일이 일어나느냐?
'회전' 합니다.
여기서 혼동하시는 분이 많은데 월드는 월드가 중심이고 카메라는 카메라가 중심이라서,
그 안에 있는 버텍스들이 회전과 이동을 해서 그렇게 보이게 만들어 주는 겁니다.
여기서는 이동은 일단 생각 안할거니까 회전만 생각하자구요.
즉 다시 설명해 볼께요. 아래 왼쪽것이 오른쪽 것 처럼 보이게 하려면 뭘 어떻게 해야 한다고요?


맞아요 '회전' 하는 겁니다. 그럼 되는 거예요.
대충 아래처럼 이케저케 컴퓨터가 회전을 시켜주면 ㅋㅋ
그럼 뷰 좌표계가 되는 거라고요. (아래 그림은 내가 손으로 한거지만 ㅋㅋㅋ)

그럼 좋아요. 월드 -> 뷰 행렬은 뭐다? (이동은 생각말고)
회전이다!! 를 알게 되었어요.
그런데 어느 방향으로 회전이다?
다시 쉽게 생각해보죠. 이번엔 탑 뷰로 비유해서 볼게요
카메라가 이렇게 옆으로만 45도에서 회전해서 찍는다고 보죠.

그럼 이렇게... 뷰의 기준이 회전하죠?
오른쪽으로 45도 정도 회전하였네요 .
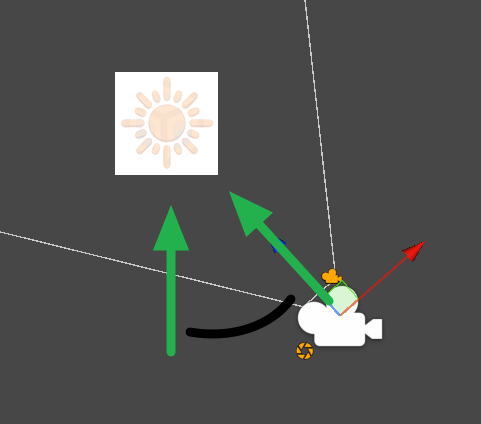
뷰의 기준이 회전한다= 카메라 뷰가 된다.
근데 진짜 카메라가 뿅 생기는 거예요? 아녜요 그냥 뷰는 가만 있고 물체만 도는 거예요 좌표는 여전히 고정이니까요.
이걸 시뮬레이트 하면 어떻게 되어요? 오른쪽 45도에서 보는거니까..
아래처럼 돌아간다라고 생각하면 되지요.
어디로 돌아요? '왼쪽' 방향으로 돌죠? 카메라가 있는 방향의 반대로 물체를 돌리면 되는거예요!!! 이게 핵심임.

즉 아래 변환이란 사실은

사실은 이렇게 되는 거였어요.
아니 기울어진 좌표계를 만드는게 더 어렵겠다..
물체를 돌리면 되는거였죠. '카메라가 있을거라고 여겨지는 반대방향으로 물체를 돌린다"
"카메라가 오른쪽에 있으니까 왼쪽으로 회전시키면 카메라 공간이 되는거야"
다했네 다했어

즉 (이동을 생각 안하면) 월드 -> 뷰 행렬은 카메라 방향의 반대 방향으로 물체를 회전시키는 것 뿐이었단 말입니다.
꼐쏙.
'Shader ' 카테고리의 다른 글
| 빌보드(Billboard)를 만들어 봅시다 3부. 마무리해 봅시다 / HLSL버전 (0) | 2024.07.28 |
|---|---|
| 빌보드(Billboard)를 만들어 봅시다 2부. 이제 진짜 만들어 봅시다 (0) | 2024.07.28 |
| Lit 셰이더 분석 2 (0) | 2023.10.10 |
| Lit 셰이더 분석 (0) | 2023.09.28 |
| 매크로 상수 배열 정의하기 (0) | 2023.02.15 |




댓글